机器学习笔记
机器学习中一些笔记和截图
学习笔记
概率,统计,随机过程
摘自这里 但是依然需要说明一下。 我们从不同的视角。
- 英文
1)The basic problem that we study in probability is: Given a data generating process, what are the properities of the outcomes?
2)The basic problem of statistical inference is the inverse of probability: Given the outcomes, what can we say about the process that generated the data?
来自 Lary Wasserman 的 《All of Statistics》
- 中文
概率和统计其实从相反的角度解决不同的问题。
概率是基于已知的模型/分布,来预测数据(预测某个事件发生的可能性,或者称之为随机变量在不同值的可能性,也即概率密度函数。其自变量是随机变量,而y则是可能性)
而统计,解决的是已知了数据(部分数据,或者称之为样本,或者称之为已知了事件的概率,或者称之为已知了随机变量的值)反过来推导出完整的模型(包括分布模型和参数)
- 理念
概率论永远认为小概率事件是会发生的,只要重复次数足够多。 而统计永远认为小概率事件不会发生,直接忽略,进而典型的基于最大似然来拟合模型和参数
- 数学思想
概率论是基于推理,演绎的思想。 而统计则基于归纳的思想
- 哲学
概率论是由因到果,探讨天命 而统计则是由果回因,反思本原。
- 随机过程:
随机过程太复杂,基本是研究生课程里的老大难了。 简单而言,确定过程,就是普通的基于时间t的函数,给定时间t,可以确定的得到y的值,而且该过程可以无限重复而得到一致的结果。 比如,宏观物理的定律。 如自由落体 s=gt^2⁄2, 在任意时刻t,我可以确切的知道s。而且不管在地球何处,也不管是重复做几次,都是这个结果。
而随机过程,由于是过程,所以依然是时间t的函数,但是,现在其应变量y,则给出的是概率,是分布,而不再是确定的值了。也就是说,随机过程研究的,是持续的,连续的概率问题。 如果拿高大上的量子力学来做例子,其波函数就可以一定程度上近似理解为随机过程,给出时间t时粒子在空间不同位置的概率分布。
线性相关和线性无关


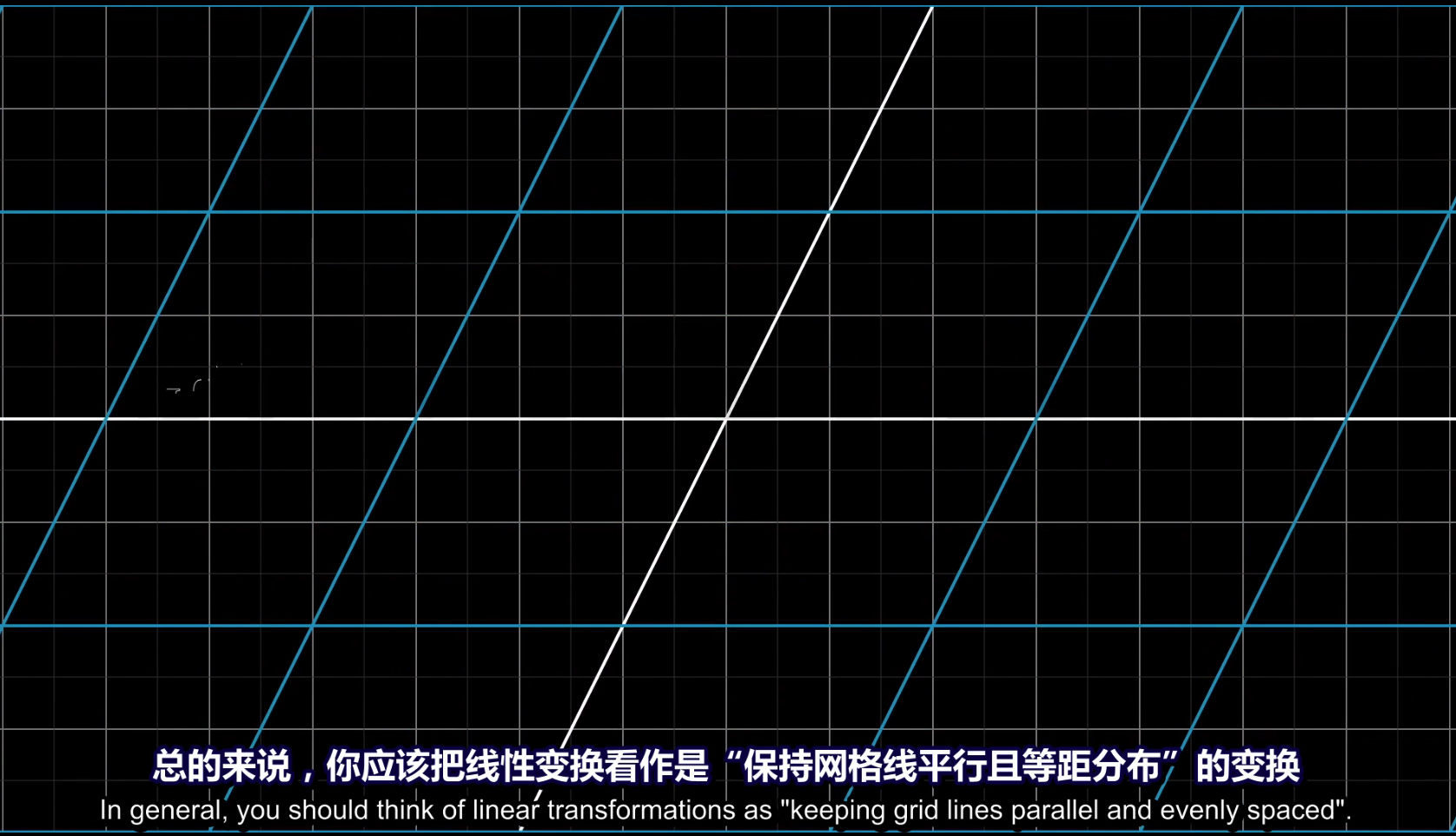
(矩阵) 线性变换
严格意义上说,线性变换是将向量作为输入和输出的一类函数

神经网络最近的发展

神经网络规模增长速率

深度学习定义

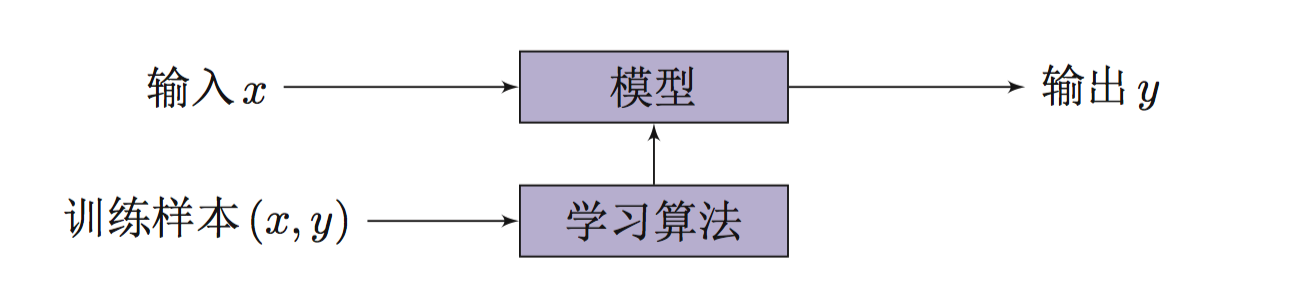
输入 输出 训练样本 模型 学习算法 关系的简单示意图
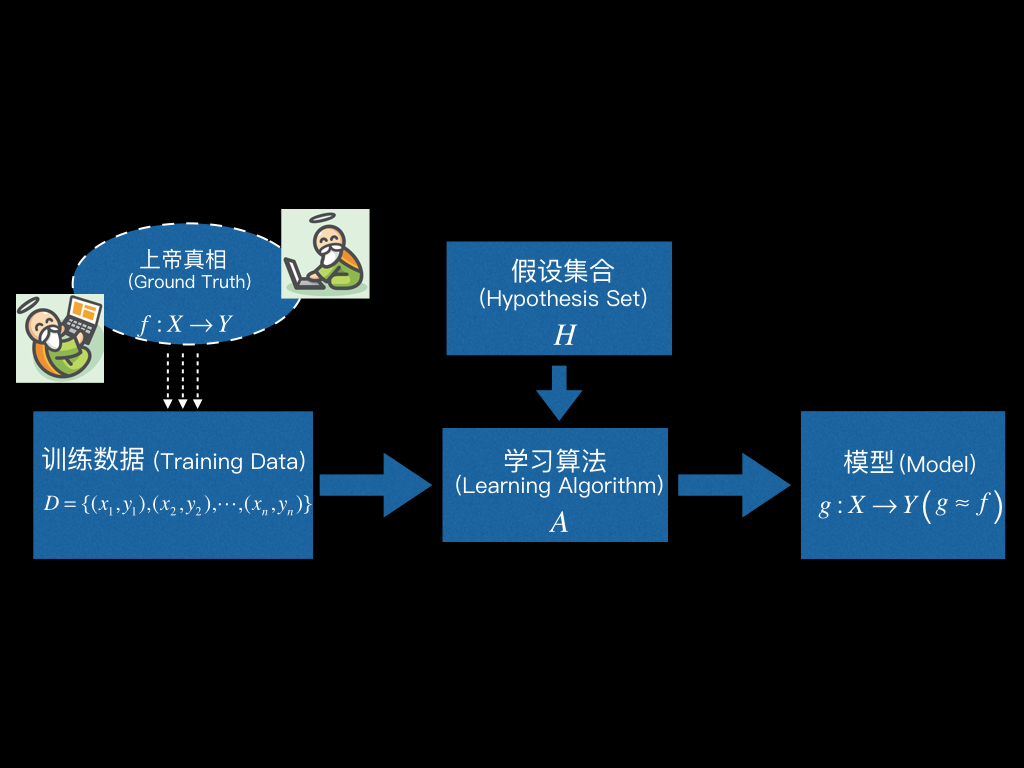
学习算法 模型的完整描述示意图
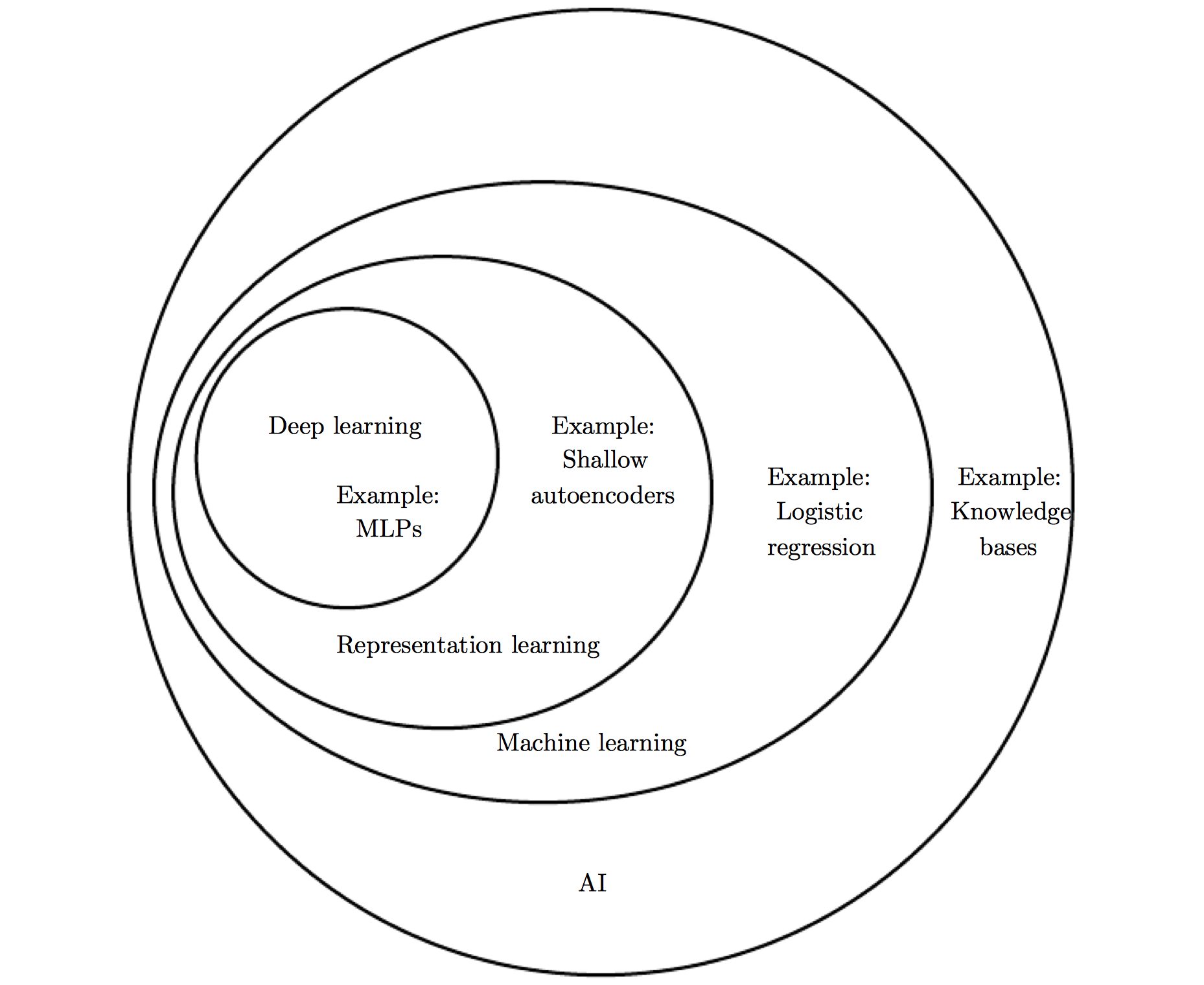
深度学习 机器学习 人工智能关系示意图
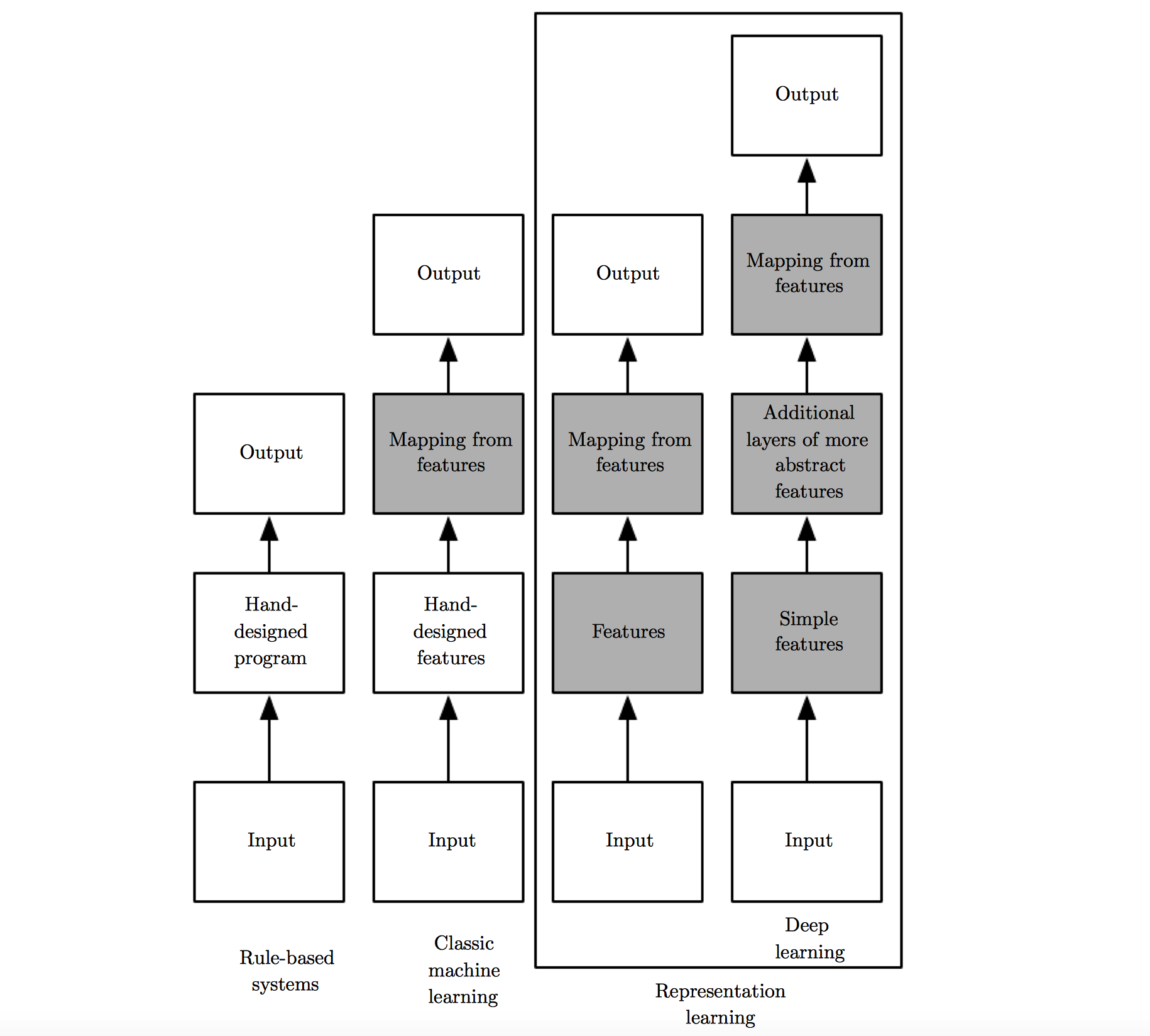
人工智能 输入 输出 方式 特征表示的发展
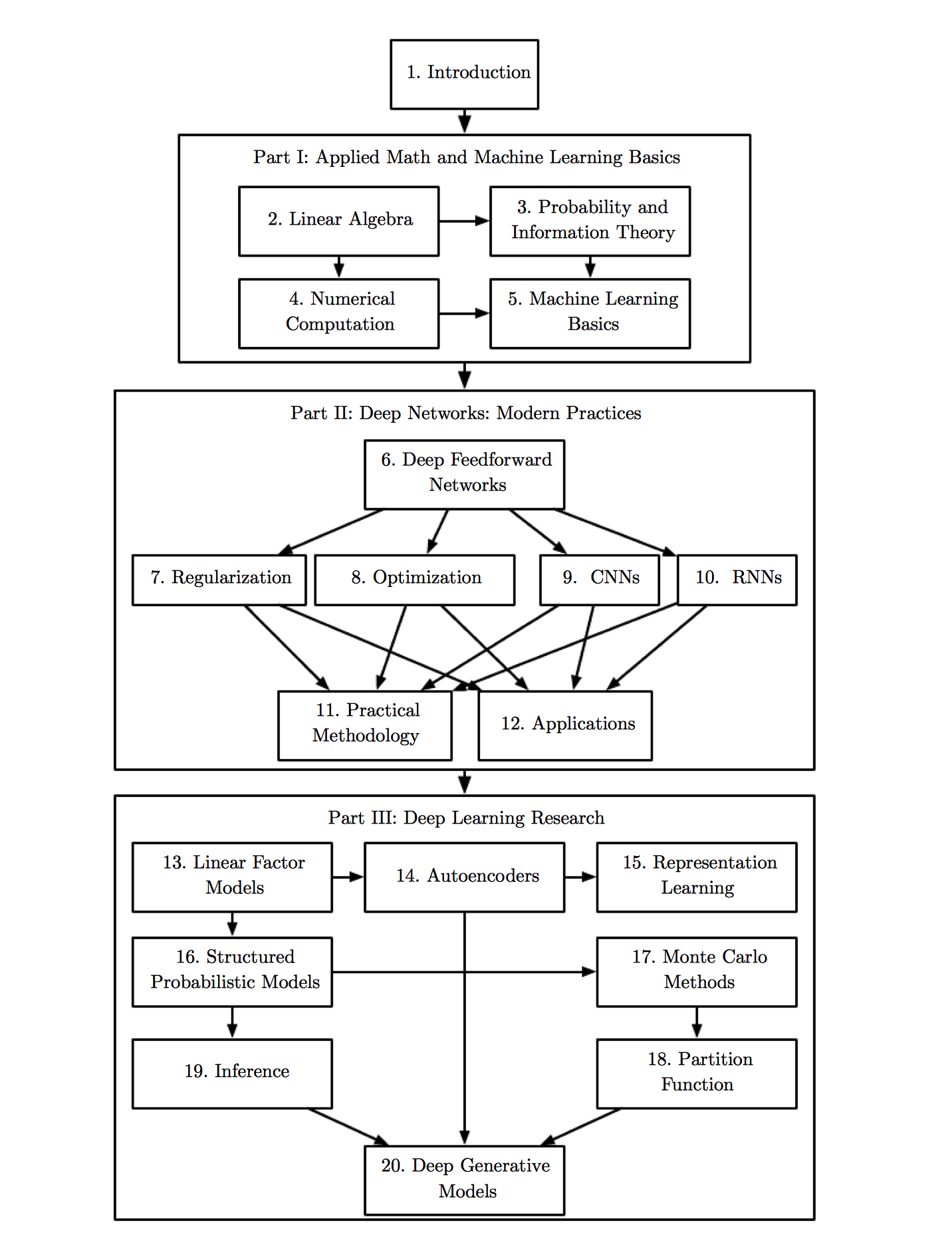
《Deep Learning》 目录
模型 策略 算法


为什么要训练集独立同分布
为什么机器学习中, 要假设我们的数据是独立同分布的 答案摘录: >用来训练的样本点具有较好的总体代表性。为什么要有总体代表性?我们要从已有的数据(经验) 中总结出规律来对未知数据做决策,如果获取训练数据是不具有总体代表性的,就是特例的情况,那规律就会总结得不好或是错误,因为这些规律是由个例推算的,不具有推广的效果。通过独立同分布的假设,就可以大大减小训练样本中个例的情形。
机器学习并不总是要求数据同分布。在不少问题中要求样本(数据)采样自同一个分布是因为希望用训练数据集训练得到的模型可以合理用于测试集,使用同分布假设能够使得这个做法解释得通。由于现在的机器学习方向的内容已经变得比较广,存在不少机器学习问题并不要求样本同分布,比如一些发表在机器学习方向上的online算法就对数据分布没啥要求,关心的性质也非泛化性。
统计学习的重要性

指示函数与符号函数

导数相关
