《写给大家看的机器学习书》
知乎专栏: 写给大家看的机器学习书 链接与摘录笔记
第1、2篇 机器学习基础概念 第4、5、6篇 机器学习可行性 第3篇 PLA感知机学习算法 第7、8篇 线性回归
第一篇 基本概念 上
这是系列文章的第一篇,我们首先介绍了机器学习的基本概念,机器学习的三个要素:数据,学习算法,还有模型。
然后我们揭示了机器学到的模型,本质上就是一个映射,或者函数。
最后我们总结了机器学习适合解决的问题,是那些难以用规则解决的问题。并且机器学习的必要前提不仅是有大量的数据,而且需要数据中确实存在隐藏的某种规律,机器学习才能帮的上忙。
第二篇 基本概念 下
传统的算法设计是根据给定的输入和目标,设计求解的计算过程。机器学习中涉及的算法则是用一种参数化的方式设计这一求解过程。因为机器学习的目标是generalization,我们希望得到一个在未来能多用几次的模型;而传统算法在大多数情况下都是为具体问题设计的,力求一次性解决问题。机器学习通常会基于一些假设,带有一种强烈的玄学色彩。
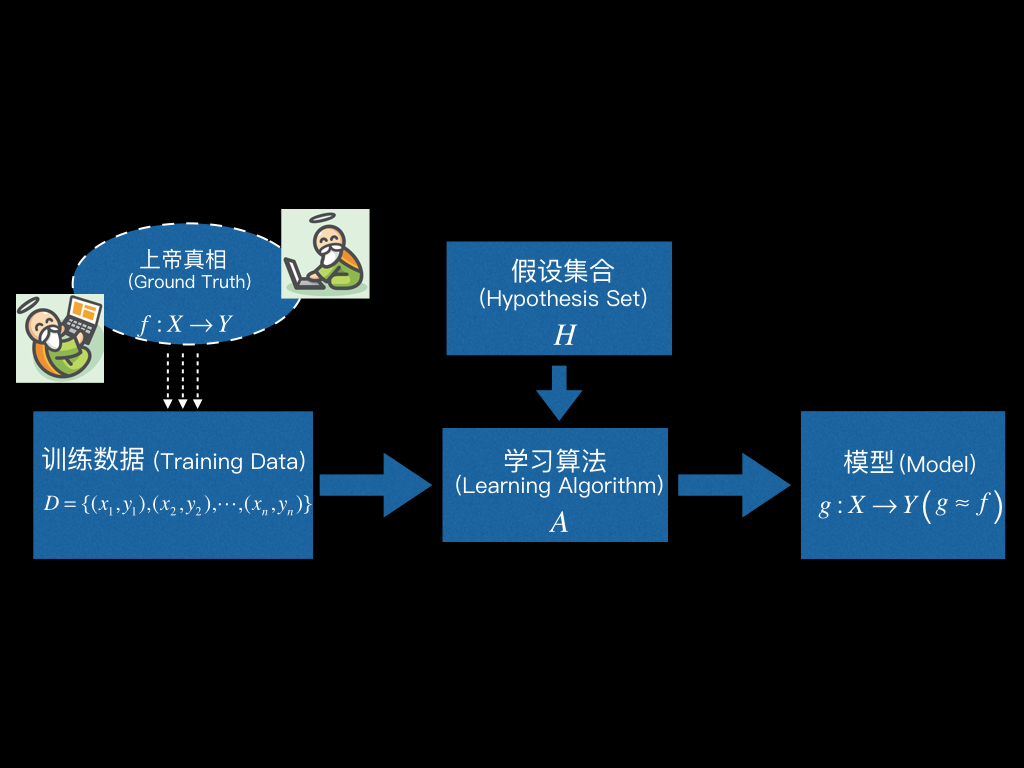
看着上图就可以用一句话来定义机器学习
Machine Learning:Use training data to compute model g that approximates Ground Truth f.
学习算法 (Learning Algorithm) 根据训练数据,从假设集合 (Hypothesis Set) 中选出最优的那个映射g:作为最终学得的模型,使得g越接近f越好。
第三篇 PLA 感知机学习算法
PLA(感知机学习算法),全称 Perceptron Learning Algorithm。其中 Perceptron 译作感知机,它是人工神经网络中最基础的两层神经网络模型。
这一篇我们将介绍PLA的假设集合,看看PLA的假设集合中等着被挑选的候选函数长什么样。看过PLA假设集合的函数表示之后,重要的是理解PLA假设集合的直观解释,事实上之所以把PLA作为第一个学习算法,就是因为它有着非常直观的理解方式。
PLA 的基本想法是每个特征都有个权重,表示该特征的重要程度。综合所有的特征和权重计算一个最终的分数(线性组合),如果分数超过某个阈值 (threshold),结果为1,否则为-1。
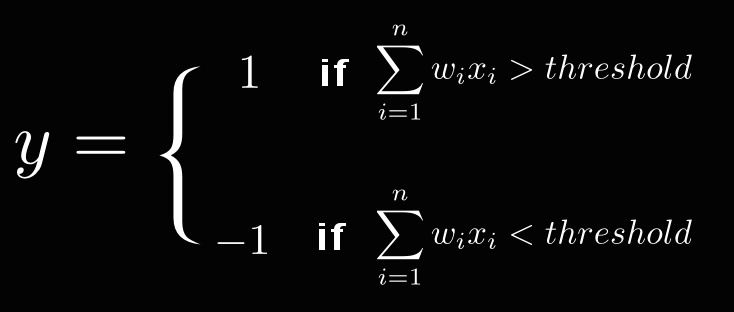 等价于:
等价于:
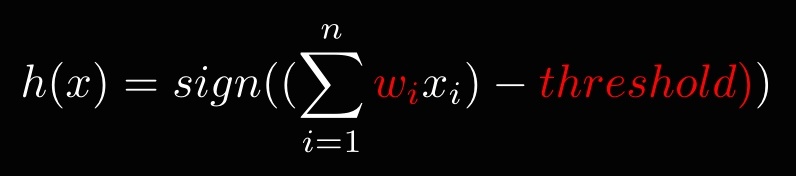
在算法完成学习之前,函数中的w_i和threshold是未知的,不同的w_i和threshold值对应了不同的函数,事实上所有可能的w_i和threshold所代表的函数集合,构成了PLA的假设集合(Hypothesis Set),叫做 Perceptron Hypothesis 。而 PLA 算法要做的,就是根据训练数据找到最优的w和threshold。
PLA 的假设集合 (Hypothesis Set) 就是所有可能的h(x)
直观形象化理解:
简化->降维
假设输入只有两个特征(二维), h(x):
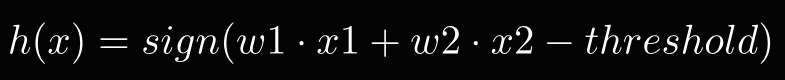

更多维的(直线变成平面、超平面)可以类比二维平面来理解,都是一种划分,基于以上特性,Perceptron是一种线性分类器,二分类的线性分类器。线性理解成特征向量线性组合还是线性划分?貌似都可以。打个问号。
PLA 具体是如何确定最优的w和threshold,得到最优的那条线的?
h(x)简化变形:

这个变形的目的是把参数threshold统一收进w,于是 PLA 找到最优的那条线就等价于找到最优的参数w。
于是 PLA 算法就可以写得相当简洁,仅有如下4步:

就是这么简单,PLA的基本思路就是:先随便找一条线,如果没能正确切分,就修正一点点,直到所有的1都在右边,-1都在左边。

事实上,如果训练数据本身就不存在任何一条线能将其正确切分,那么 PLA 无论如何也无法找到理想的直线。学习将进入永不停止的循环。
训练数据至少存在一条直线能将其切分开,称为训练数据是线性可分的 (Linear Seperable) 。
训练数据是线性可分的 (Liner Seperable) ,是 PLA 能够学习的必要条件。
在现实中,哪怕原本的训练数据产生于某个“上帝真相”并且是线性可分的,在收集数据处理数据的过程中不可避免的会引入一些脏数据,这部分错误的训练数据我们称为噪声(Noise)。
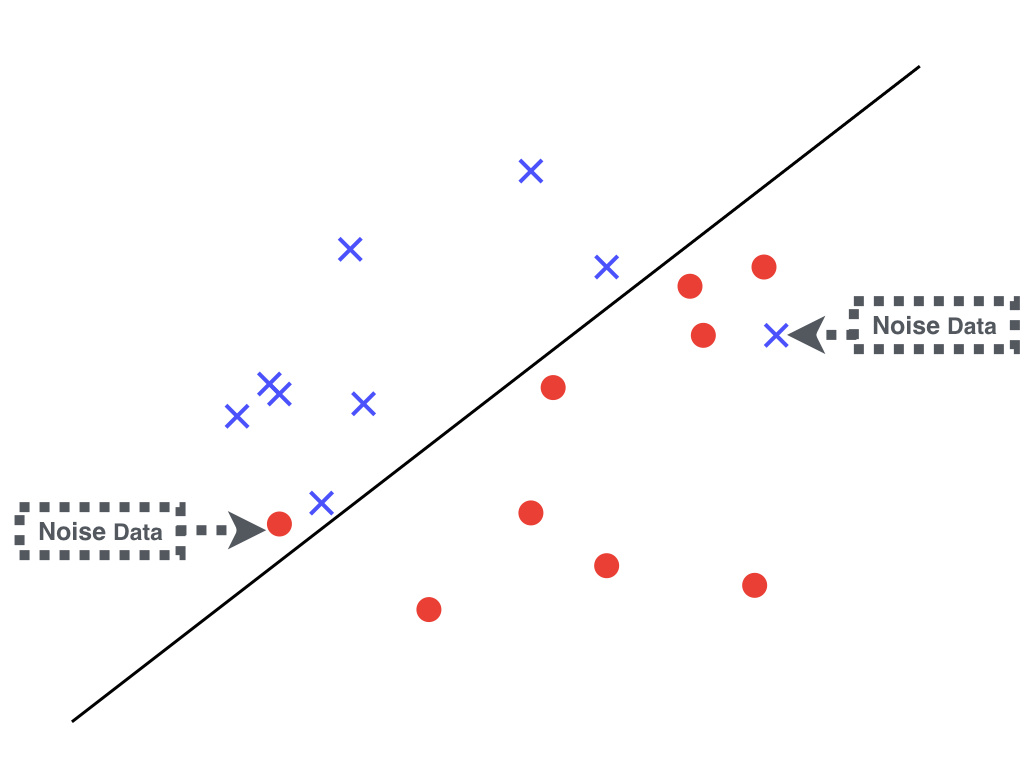
针对这种噪声数据引起的,原本线性可分的训练数据变成了不是线性可分的情况,有一个升级版的 PLA 算法,只需要增加简单的两步节能解决问题:

怎么衡量表现的好坏?? -> 犯错率

TODO:
- 要找时间代码实践PLA!!
4、5、6篇是关于机器学习可行性的理论知识,暂时关小黑屋了,放到最后。。。
第七篇 线性回归 上
线性回归(Linear Regression)


Q: 线性回归模型里面为啥要有一个阈值 (threshold)?PLA模型中能理解 模型计算出一个分值超过某阈值 为点击 或不点击
A:因为一条直线需要有个常数项 否则不能满足:空间中任意一条直线都用这个hypothesis表示 (加阈值才能表示所有的回归可能)
线性回归的直观形象理解: 依旧是降维和类比来理解
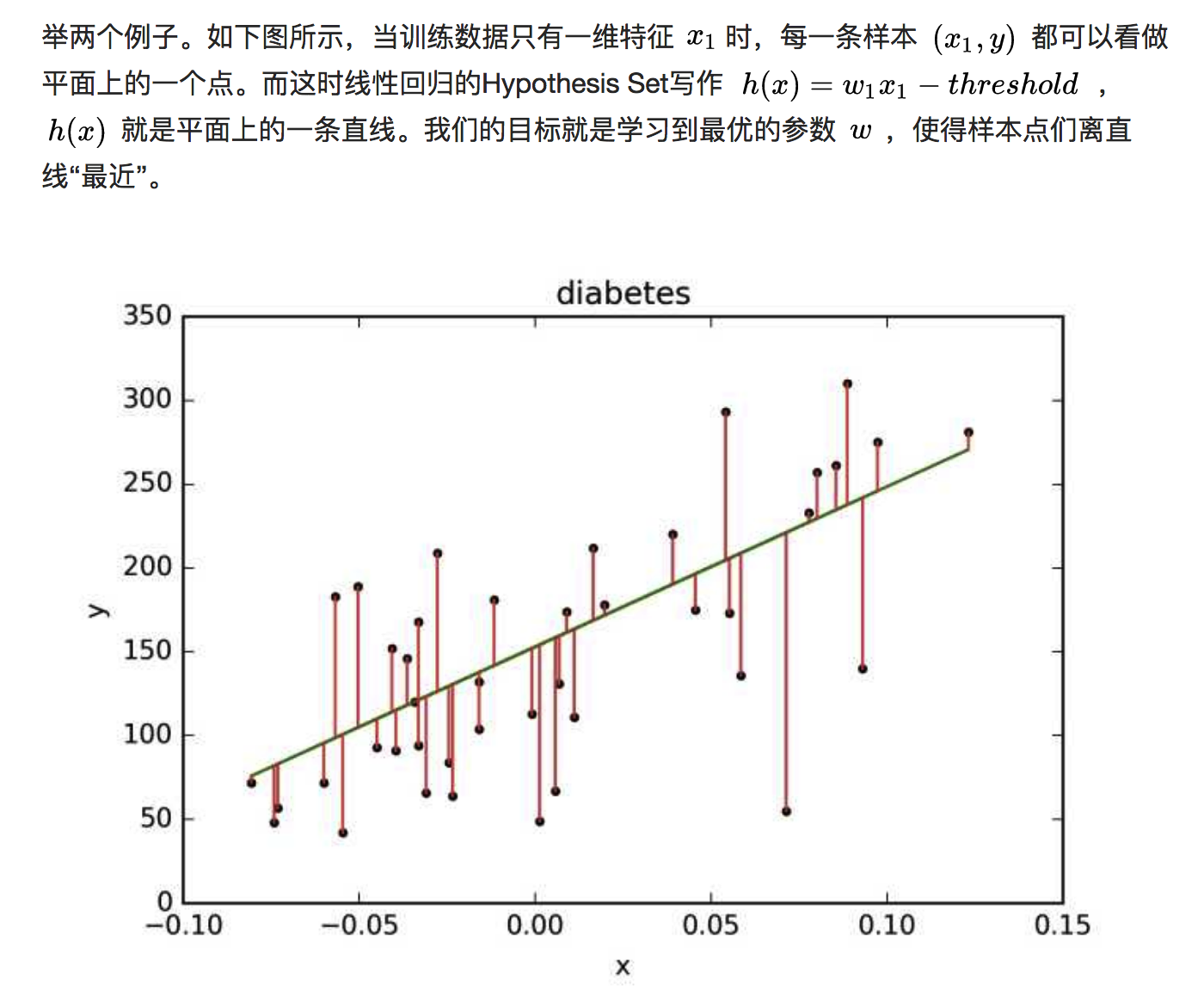
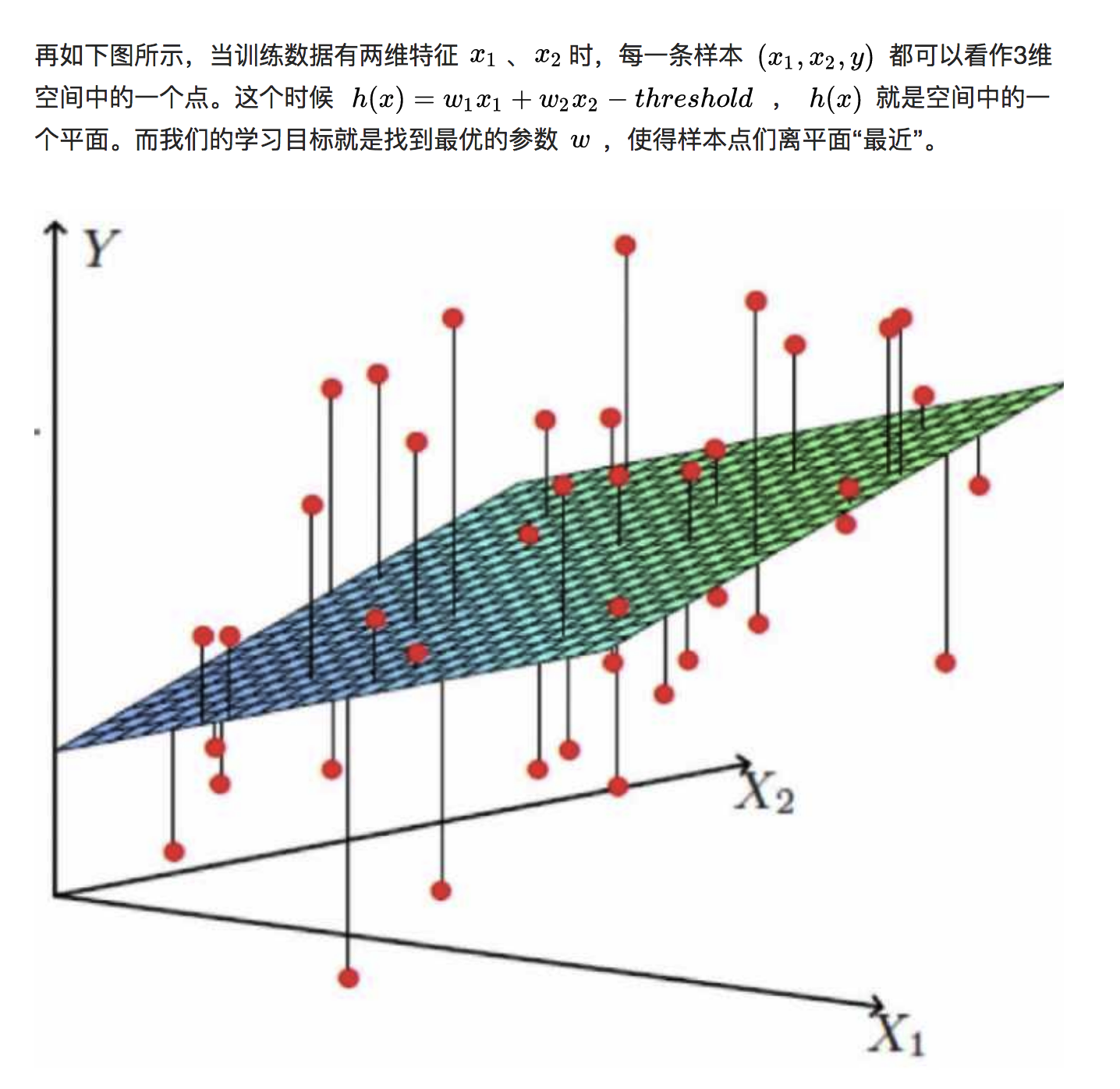
由此推广到更高维度上,虽然没办法再想象了。。类似想象高纬度的宇宙,但数学是高度抽象的,表达能力极强的,爱因斯坦的想象力也要数学来实现,如广义相对论的诞生
怎么表示近呢??

对于任意样本标注 (x,y) 和模型的预测值 h(x) ,均方误差表示为标注值 y 和 预测值 h(x) 差的平方:Error=(h(x)-y)^2 所以,我们的目标是对于训练数据中的所有 N 个样本点,使平均均方误差(损失函数)最小。
第八篇 线性回归 下
Loss Function 定义了模型的好坏评估标准,我们说学习算法从 Hypothesis Set 中选出最优的那个模型,其实就是找出另 Loss Function 最小的 Hypothesis。
keyword: 最小二乘法

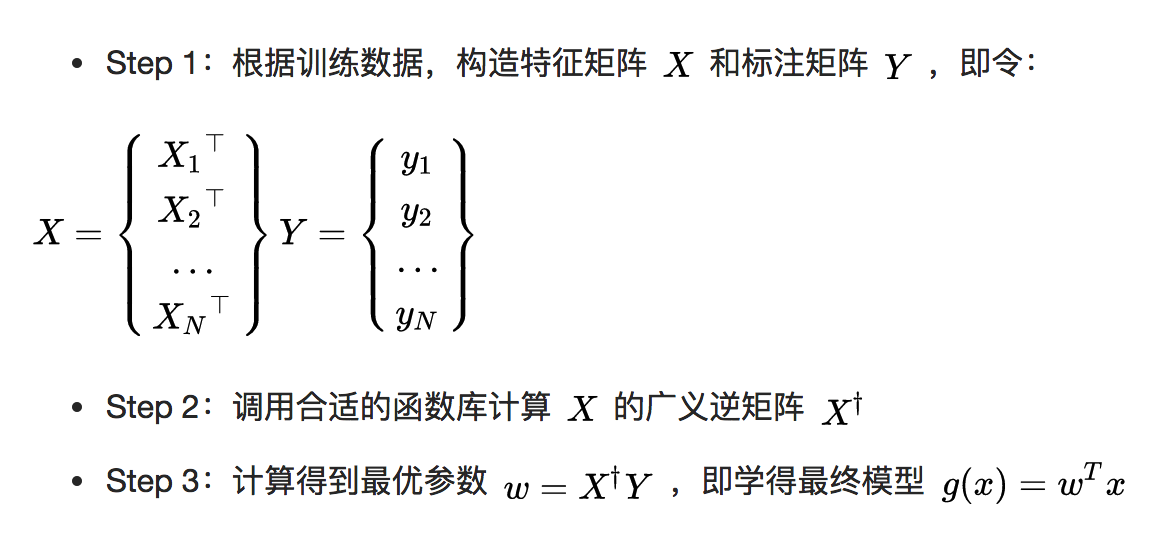
实际使用线性回归非常简单,仅有三步:
PLA vs 线性回归

第四篇 机器学习的可行性 上
没有免费午餐定理 No free lunch theorem
沃伯特,原名 David H. Wolpert,他提出并证明了 No Free Lunch 定理的科学家。No Free Lunch,即天下没有白吃的午餐,是所有机器学习专家求学路上的一记板砖。
NFL定理在阐述的过程中假设了f的均匀分布,即所有潜在的可能性发生的概率是一样的。
在不知从哪儿来的训练数据的情况下,可能产生训练数据的Ground Truth f有多个,但又因为没有具体的场景,导致这多个f是真正产生这批训练数据的Ground Truth的概率是一样的。
而无论哪种学习算法必定最终倾向了其中的某个f,因此最终这些算法的期望水平就是一样的。(学习算法的这种倾向,称为学习算法的归纳偏好(inductive bias),简称偏好。)
在具体的实际场景中,某些f代表的可能性发生的概率大,某些f代表的可能性发生的概率小,某些可能性则根本不会发生。它们的概率不是均等的,因此不再满足NFL定理的前提。
BRAVO! 概率拯救了世界,拯救了机器学习!
在具体的现实问题中,那些归纳偏好与问题本身匹配的算法就能取得很好的效果,从而令学习是可行的。
NFL定理背后所表达的哲学与实际意义: >脱离具体问题讨论机器学习算法的好坏,是没有意义的。
第五篇 机器学习的可行性 中
计算学习理论 (Computational Learning Theory) 回答的是机器学习为什么可以学习的终极疑问,它是机器学习的理论基础。
当 Hypothesis Set 中只有一个 hypothesis 时,模型的预测准确率与训练准确率的关系可以类比成一个相当好理解的例子——人口调查。
要调查某省总人口中的男性比例,自然不可能去统计总人口数和男性的总人数。常见的方法是进行科学的抽样,抽样所得的男性比例即可近似作为总人口的男性比例。这样做的科学性是由著名的【Hoeffding 不等式 (hoeffding’s Inequality) 保证的。





第六篇 机器学习的可行性 下
关键词:
- dichotomy
- 成长函数 Growth Function
- Break Point
- VC Dimension
TODO:
- 4、5、6篇是关于机器学习可行性的理论知识,了解不深,找时间补足。